How Computers Actually Work
Transistors
Transistors are the most basic, essential part of a computer. A transistor is simply a switch that can be switched on or off using an electric signal without human intervention. The way it works is just a bit of chemistry but that’s is irrelevant.
This is the most common transistor (NPN transistor):
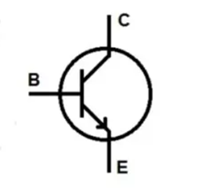
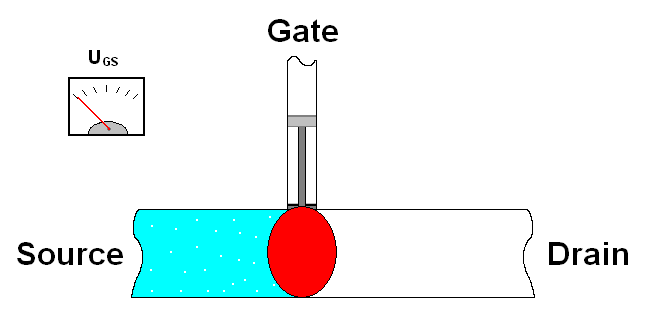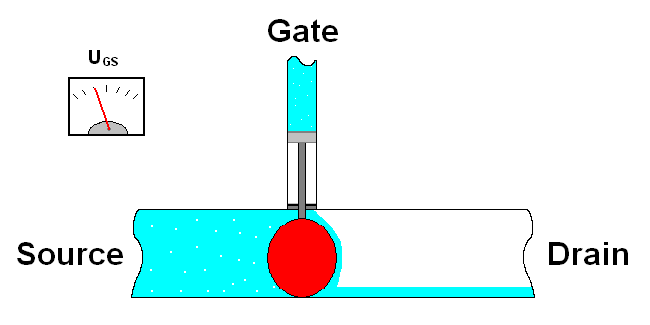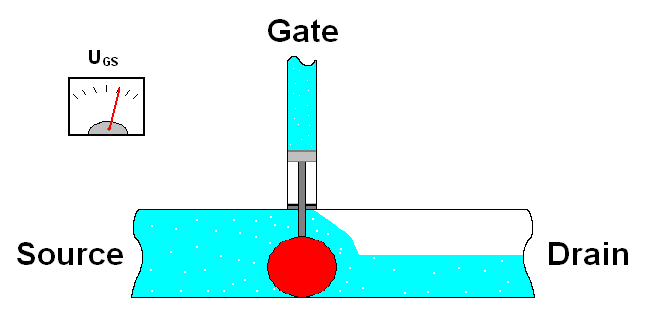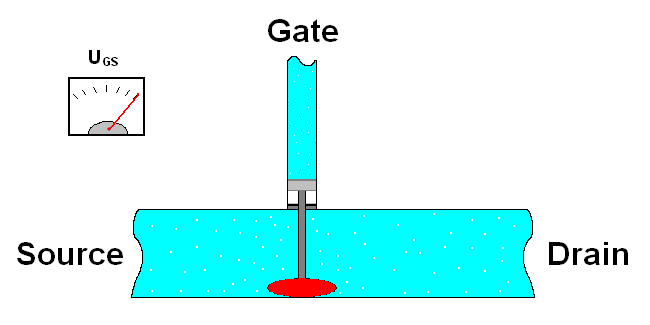
Consider C and E as one wire and B is a switch between them, when B is on, the “switch” is on, so current flows from C to E. When B is off, C and E are technically off/disconnected/no current flows.
Logic Gates
Everyone was told, at some point or another, that computers work with 0’s and 1’s, but all that means is that computers perform logical operations using electricity and can therefore be either on or off (mathematically speaking you can perform operations with 3 states or more but there is a risk of error, this is to be explained later). Logic gates simply perform any arithmetic or logical calculation required by a computer, the only reason we can make logic gates work on their own was the creation of the transistor. Here are the major logic gates:
AND Gate
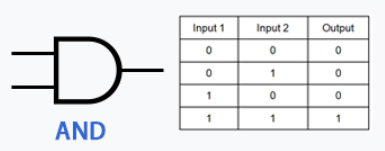
In words: The output of the AND gate is only on if both inputs x AND y are on, as you can see from the table next to it, when either inputs are off, the output is off
As a proof of concept, here is how an AND gate is made with NPN transistors

The current flows from Vcc to Gnd, only when both A and B are on, does current pass through T1 and T2, thus making the output on.
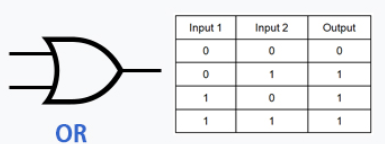
OR Gate
This is the OR gate, as you can see it is only on when x OR y is on, it is not on when both of them are off
And again for proof of concept, here is an OR gate with transistors:

You might notice the similarity between it and the AND gate, but here they're “criss crossed” so that if either A OR B is on the output is on.
NOT Gate
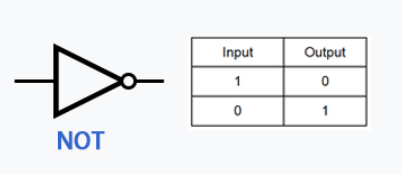
Now for the NOT gate, it is only on if X is NOT on, basically it just inverts/flips the input
For proof of concept again:

Its circuit is a bit difficult to explain but it works anyways, it is shorted to being on by default, until A becomes on, Then the output becomes NOT A (or off)
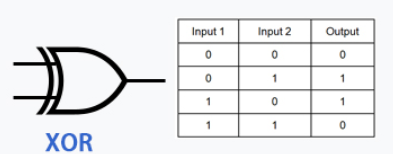
XOR Gate
Now for the XOR gate, it stands for Exclusive OR, as in it is ONLY only if X OR Y is on, if both are on it remains off
Inverted Gates
The reason they’re very versatile is that you can connect them to each other, this allows you to do many things, but very importantly, you can connect the output of any of the previous gates to the input of the NOT gate to invert it, which allows you to make the following logic gates:
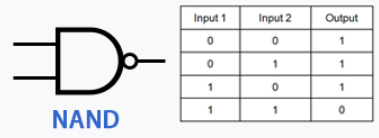
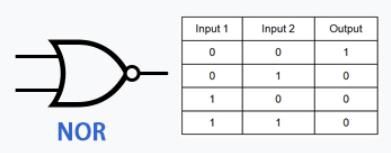
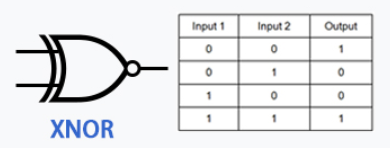
As you can see this allows for a lot more combinations.
Arithmetic Functions with Binary
Now you need to do arithmetic functions with a computer, so addition, subtraction, division, and multiplication. So a bunch of nerdy mathematicians made the binary system, we use the Denary system (The word denary is based on the Latin word dēnārius, which means "containing ten"), simply because it is made of 10 possible numbers (0-9), you go from 0 to 9 and when you run out of numbers you add a one to the left side (tenths place, aka 10 times more in value than the ones place, because you have 10 possible digits), and then you put a 0 (the smallest digit) in the ones place… so it becomes one zero, aka 10. Then you add 1 to 9 to that (so 11, 12, 13… 19). Guess what, in the Binary system (The prefix "bi-" in "binary" means two. It comes from the Latin word bini, which translates to "two by two". ) you have only two digits, 0 and 1, you do the same thing to write numbers in binary as you do in denary.
You first have 0, then 1, then you run out of numbers so you put one in the “two’s place” (instead of the tenth place in denary), so the number in the “two’s place” becomes twice as big as the number in the ones place. So you go from zero (0) to one (1), to two (10), then to add 1 to (1), so it becomes 11 (3 in binary). The places in binary double each time.

This is equal to 64+16+8+1=89 in denary and so on
Binary Addition
This is the process of addition in binary:
- 0+0=0 (zero)
- 1+0=1 (one)
- 1+1=10 (two)
- 1+1+1=11 (three)
And you use the regular denary addition system, so for example:
110110 + 11010
(which is 54+26 in denary)

How do you convert this Denary?

And to confirm, yes 54+26=80
Guess what, there is a circuit that adds binary using logic gates (which use transistors).
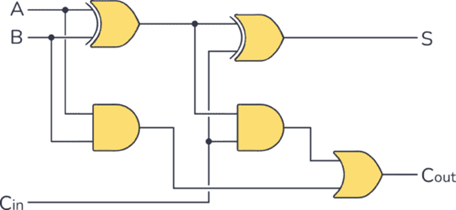
Have a look at this, A and B and Cin (Carry in) are inputs, and S (sum) and Cout (carry out) are outputs. if you attempt to add any combination of A and B, the value will be correct, now this can only add two bits (a bit is a single digit of binary), what if we want to add more? We can repeat this circuit and connect the Cout of Circuit 1 to the Cin of Circuit 2, we have successfully made a chain of adders, and can add 4 bits. This can be done infinitely and therefore we get to the level of a modern 64 bits computer.
Now as a proof of concept, you can make a lot of things with transistors and logic gates. Now there are circuits that add, subtract, multiply, divide, do logic manipulation (so for example 1001 AND 0111 = 0001, theres OR and XOR and NOT and so on…).
Now there is something called a multiplexer (MUX) (also made out of a lot of logic gates), This chooses the operation to be done by the CPU, so for example you have 2 inputs, and circuits to add, multiply etc.. next to the numbers to be added, there would be a “Flag” signal that tells the MUX (multiplexer) to add, the multiplexer will in turn only return the result for addition. This result is then used for other operations until the program does what it needs. For context just moving a game means calculating the change in distance for example, this is therefore calculated as OriginalDistance+DistanceNew for example, this would be what a programmer sees, what actually happens is that the CPU takes the value of Original distance and Distance New from RAM, copies it somewhere closer (in storage that is a lot faster called cache), the values go to the MUX along with the flag that says it wants to add the two numbers, the this result is stored in RAM to be accessed by the game, this is just to go from point A to Point B in a 1D game, let alone 3D games, billions of calculations are performed per second in this way.
And since you now know logic gates anyways, they can be used to change or identify a bit, so for example if you want to set a bit to 0 and you don’t know if it is a 1 or a 0, you can do the bit AND 0, since anything AND 0 = 0, you are sure that the bit is 0 (you being the computer).
How do computers store data?
Firstly, you need to understand the logical flip flop (please don’t say it, ty), it looks like this:
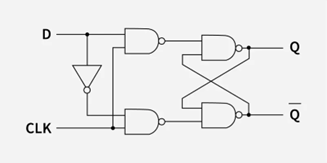
The CLK (Clock signal) is a square wave signal that looks like this:

The flip flop stores the value of input D in the form of Output Q. it only refreshes the value of Q from D when the CLK signal Is high or 1 (the clock is a very high frequency signal), Whenever the clock signal is low, the value of Q remains the same and hence the value of D is “Stored” in the flip flop.
Now guess what, connect billions of these to each other, maybe into 64 bit segments (the modern computer is 64 bits) and then you have RAM and registers for the CPU to “retrieve” or “store” (read/write respectively).
How are all operations synchronized?
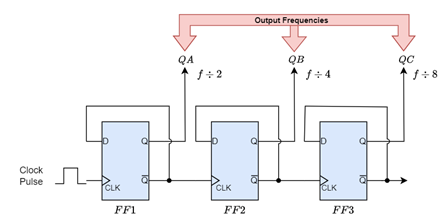
The CPU (or practically motherboard) has a quartz clock that uses a quartz crystal to generate a very fast clock signal with a known frequency, this frequency is constant and all component of the CPU and even the RAM uses a factor of that frequency to operate, fore example, modern CPU’s can run at up to 6GHz (yes 6 BILLION times per second). Factoring out a signal is as simple as using Flip Flops to halve the signal (which can be done multiple times to reach the required frequency). This can be done with D-Type Flip Flops as shown below (btw Q Not is just Q inverted):
What does programming a computer actually mean?
Code is split into 2 things, instructions and data, the instruction bit act as flags which tell the CPU components (a MUX for example) what operation to perform, and the data is either the immediate binary value or a memory address at which the data that is to be processed (added to/subtracted from for example) is stored. So programming is literally just storing the individual instruction and data bits in a way or another (let’s say RAM or registers). The CPU accesses the RAM to know what it should do, and it does it 🤷♂️.
Oh and yes CPU’s have no clue what they’re running or doing (so please don’t trust AI ok 🙂).
How a CPU Works (Simplified)
Now that you know ALL of this, here is how a CPU works:
It has a bunch of cores connected to each other, and each core contains the following:
- ALU (Arithmetic Logic Unit): has Addition/Subtraction/Multiplication/Division/Bitwise logic (so AND OR XOR NOT etc..), Shifters/Rotators (Basically move bits around), Comparators (Checks if something is equal to/less than/greater than another thing using logic gates again), and finally an FPU (Floating Point Unit) which does arithmetic with real/decimal numbers, again using logic gates
- Registers: Memory units smaller but faster than RAM that are in the CPU itself for it to directly access.
- General purpose registers (stores basically any data copied from RAM if it is to be accessed frequently by the CPU for example)
- Special Registers: (All of which have a MUX which allows the CPU to pick the instruction/data to be retrieved)
- PC (Program Counter): a bunch of memory locations that are next to each other that contain a list of the instructions to be executed (in order too), when a CPU performs an instruction it increments the address to be accessed in the PC and therefore the next instruction is retrieved. The diagram below is a nice visual demosntration: it goes from address 0000 to 0001 (and therefore from instruction 1 to 2 and so on)…
- CIR (Current Instruction Register): Stores the instruction that the CPU directly accesses (the “current” instruction)
- SR (Status/Flag Register): Stores a “condition/state”, for example a certain value is 0 or there is an error, or a certain value is negative. (not very important to understand tbh)
- CU (Control Unit): Remember how the CPU accesses registers and RAM and performs instructions? The thing that actually does that is the CU, it is a series of circuits made up of Logic gates and MUX’s, used to “Fetch” the data and instructions from RAM or registers, “Decode” the instructions with MUXs to know which operation is to be performed next, and therefore “Execute” The instruction (Usually by sending it to the ALU). Also CPU’s have code that says which instructions correspond to what feature (so 1001 might be addition, 1011 is multiplication and so on, the CU uses that “table” as reference to know what to do with each instruction). A cliché demonstration/example of what actually happens in a CPU:
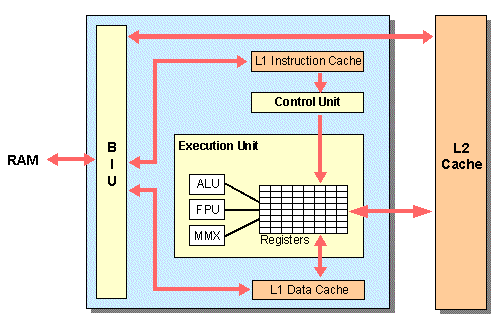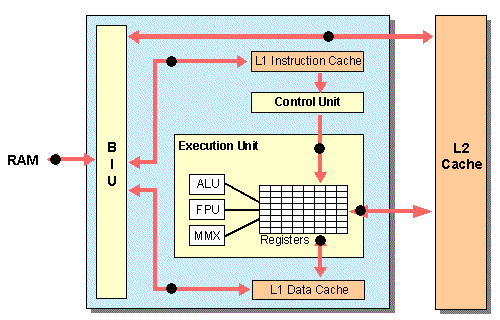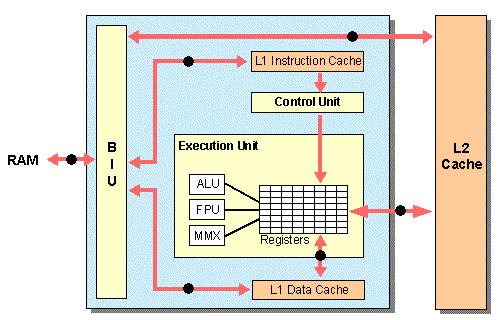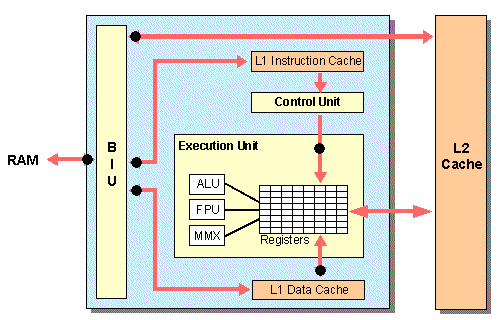
FDE (Fetch Decode Execute) Cycle Simplified:
